From neuron
to artificial neuron
to artificial neuronal nets
Experiments with an
artificial neuronal net ODANN
(free download) are described in detail. The MS DOS
Program ODANN (see 3 files above) runs under Windows XP (and down
compatible). Under Windows Vista please copy ODANN.exe into the Program:
(freeware) which includes a DOSBox. — Contact address: ewertjp@gmx.de
The experiments performed with ODANN provide insight into feature detection. Of particular
importance is the comparison of the properties between artificial and
biological neuronal nets. ODANN — in which the net's topology can be varied and neurons be eliminated — may help us to
better understand the functions of single neurons in biological neuronal
nets. For example, in a net trained with the
backpropagation algorithm functions of certain neurons emerge that are
essential for feature detection. Other neurons are important for the training; after training, the
net's performance in feature detection may be even improved by elimination
of (such) neurons. This reminds us of the ontogeny of our brain:
initially redundant development of nerve cells, —programmed
cell death thereafter.
[ODANN was awarded during the Deutsch-Österreichischer Software-Wettbewerb]
______________________________________________________________
Rationale
ODANN is a feature detecting artificial neuronal net: Object Dimensioning by Artificial Neuronal Net. It simulates the worm(W) vs. anti-worm(A) discrimination investigated in the toad’s visually guided prey-catching behavior (see http://www.joerg-peter-ewert.de/3.html). For this task, ODANN is trained by means of a backpropagation algorithm. The experimentation with ODANN allows one to study some basic properties of feature detection by comparison with properties known from biological neuronal nets.
The feed-forward topology of ODANN consists of an input matrix (retinal input), a so-called hidden layer (layer of neurons that are processing the converging input from the matrix), and an evaluation layer (two neurons that are processing and evaluating the converging input from the hidden layer) (cf.Fig.1, bottom):
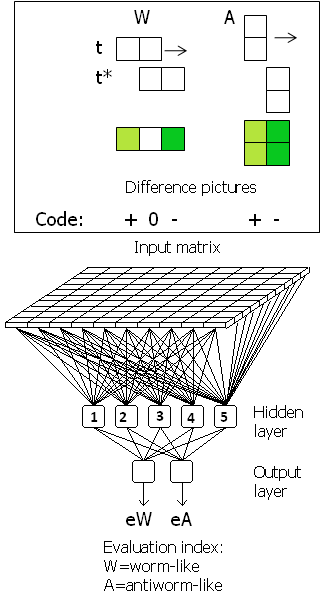
An artificial neuron i is a calculation unit. It summates the weighted (w) input x [neuronal equivalent: dendrites] from other neurons j, subtracts a threshold siand produces an output yi [neuronal equivalent: neurite and its collaterals] according to an activation function fi :
yi = fi ∑ xj *wij – si
wij and si are variables.
The experiments performed with ODANN allow one, for example, to examine
(a) the size of the input matrix
(b) the number of processing neurons of the hidden layer
(c) the relationship between (a) and (b)
(d) lesions to certain neurons of the hidden layer
and to test their influence on the learning curve and the detection acuity. Further properties of the net concern questions of
· feature detection
· redundancy
· optimization
· generalization
· interpolation
· unexpected functions (not trained)
Project A: worm vs. anti-worm detection
In order to become familiar with ODANN, please follow the experimental steps below:
[Screenshots under Vista: “Snipping Tool”; under DOS: “Strg+F5”]
Open ODANN.exe
ODANN_intro OK:
Click: Net (Netz):

Click: New (Neu):
Give the net a name, e.g.: netz1
Net options-1: Define the size of the input matrix IM ("Eingabeschicht") (edge length in pixel), e.g.: IM=10 [10 x 10].
Define also the size of the hidden layer HL ("Zwischenschicht"), e.g.: HL=5
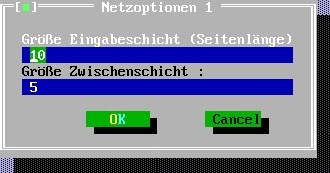
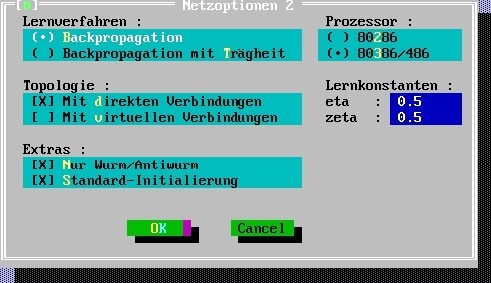
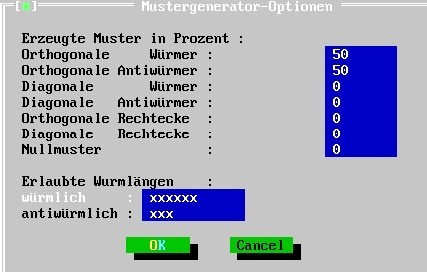
Leave the settings of the net options-2, except “Extras”: if the net should evaluate the input just as “wormlike” vs. “anti-wormlike”, put “x” for “Nur Wurm/Antiwurm”:
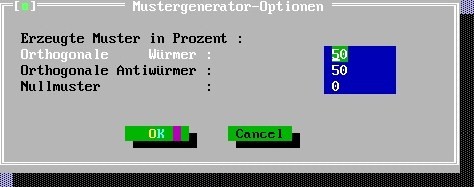
Leave settings: worm patterns ("Würmer") [50%], anti-worm patterns ("Antiwürmer") [50%], zero patterns ("Nullmuster") [0 %]:
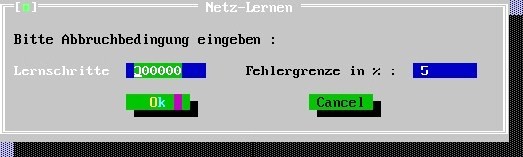
Click: training ("Lernen"):

Leave settings: training will be stopped either after 300,000 training steps or after an error limit of 5%:
The net will be instructed by means of a special program involving a backpropagation algorithm. The net can be trained to classify and evaluate bars moving as prey (worm configuration) or as nonprey (anti-worm configuration) [starting with an error of 79.80% at 0, i.e., after the 1st training step]. The evaluation is expressed by two output neurons; the upper neuron indicates the degree of wormlike (index eW) while the lower neuron indicates the degree of anti-wormlike (index eA), both indices ranging between 0.0 and 1.0.
Input matrix Hidden layer Output neurons
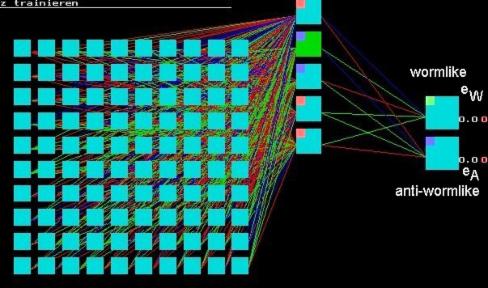
The stimuli are fed into the input matrix by means of a pattern generator that generates worms and anti-worms of different length, traversing the matrix in horizontal or vertical direction. In fact, not moving worms and anti-worms can be fed into the matrix, but their static “difference pictures” (cf. Fig.1, top): Consider the image of a moving bar at the time t and the image of this bar after an elapsed time t*. Actually, images are displaced by one pixel. The arithmetic difference between both images (for constant velocity of movement) yields the difference picture. [Stimulus of 1x1 pixel is not defined; please ignore]. — Training is complete in this case after 5,000 training steps (error: 2.50%), indicated by an acoustic signal and a blinking window.
Pushing the spacer opens a test window. We shall now test the net’s ability in detecting a bar as wormlike and anti-wormlike, respectively. There are two choices to test: (1) the difference pictures for worms and anti-worms can be fed into the matrix manually by clicking single pixels of the matrix with the left and right mouse button, each button producing a bright-green or dark-green color, respectively; reversal is possible by clicking the pixel and pushing the spacer [if no stimuli are present at the matrix, the output of the output-neurons is not defined]; (2) the difference pictures for worms and anti-worms are generated statistically in an animated fashion:
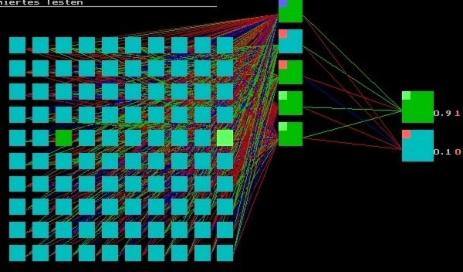
The figure below shows a difference picture of a bar of an edge length of seven pixels, traversing the matrix in worm configuration horizontally. Due to the dislocation of the wormlike bar by one pixel, the extension of the difference picture includes one pixel more; cf. also Fig.1)]. The evaluation is expressed by two output neurons; the upper neuron indicates wormlike (index eW) and the lower neuron indicates anti-wormlike (index eA), both indices ranging between 0.0 and 1.0. Red numbers (shown for animated testing) refer to the theoretic values and white numbers to the values calculated by the trained net, in this case eW =0.9 (1.0); eA =0.1(0.0):
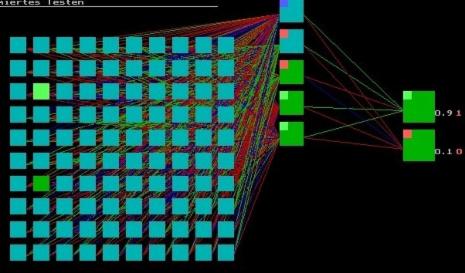
Difference picture of a bar of an edge length of four pixels, traversing the matrix in worm configuration vertically:
Difference picture of a bar of an edge length of six pixels, traversing the matrix in anti-worm configuration horizontally:
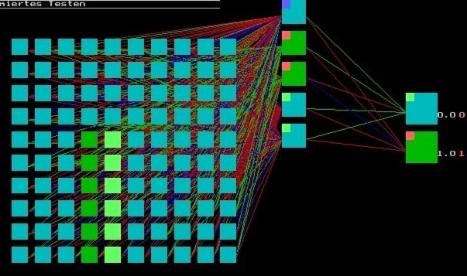
Difference picture of a bar of an edge length of seven pixels, traversing the matrix in anti-worm configuration vertically:
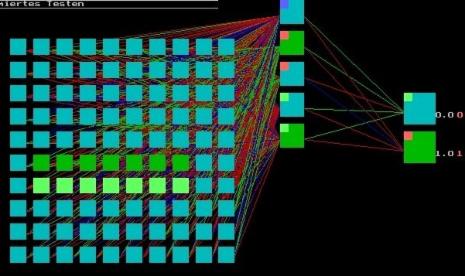
Pushing Esc opens the test window again. The learning curve can be plotted (click: “Lernkurve zeichnen”) [Screenshots under Vista: “Snipping Tool”; under DOS: “Strg+F5”].
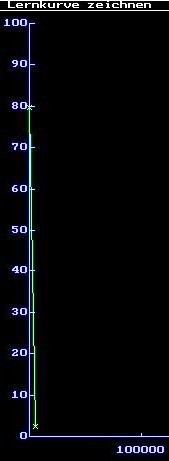
Learning curve: The net is trained after 5,000 training steps at an error of 2.50%. [Very seldom a net cannot be trained at all, it seems to be “crazy”; in such a case please close ODANN and start the program again]
To examine the neurons of the hidden layer with respect to feature detection, the program allows one to eliminate single neurons of the trained net:
Pushing Esc opens the test window. Click on lesions (“Verletzungen”) and you will return to the net again. With the left mouse button you will eliminate a neuron (marked by X) [you can reverse the marking by clicking with the mouse and then with spacer]:
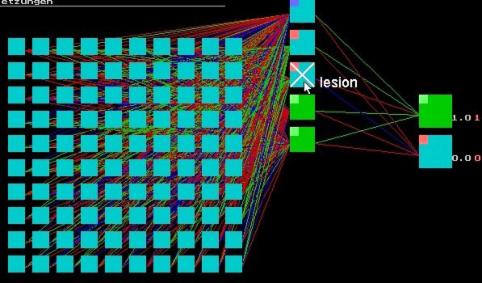
Pushing Esc, you will test the nets capability in detecting worms and anti-worms either by the manual or animated method:
Various questions should be addressed to appropriate experiments
Abbreviations: IM, input matrix; HL, hidden layer; eW ,eAevaluation values indicating wormlike and anti-wormlike, respectively; A, anti-worm; W, worm.
Experiments
(1) Is one neuron in the hidden layer sufficient for W vs. A detection? Please answer this question with a net of the topology: IM=10 (x10); HL=1. Check the learning curve.
(2) In the trained net of (1), please test the evaluation values eW and eAfor W and A stimuli, 10 stimuli each. Use the following table (work sheet) and mark the sort of classification by a cross (x):
_____________________________ _____________________________
W-stimulus A-stimulus
classified: classified:
correct mediocre incorrect correct mediocre incorrect
eW =0.9-1.0 0.6-0.8 ≤ 0.5 eA =0.9-1.0 0.6-0.8 ≤ 0.5
10 measurements
_____________________________ _____________________________
(3) Repeat experiment (1) for HL=2. Check the learning curve. Tick the classifications for W and A stimuli in the work sheet of (2).
(4) Repeat experiment (3). After training, please eliminate the upper neuron of the hidden layer. Tick the classifications for W and A stimuli in the work sheet of (2). Train the lesioned net and check the learning curve. Then repeat experiment (3); after training, however, eliminate the lower neuron of the hidden layer. Discuss the three learning curves.
(5) Repeat experiment (3) for HL=3. Check the learning curve and tick the classifications for W and A stimuli in the work sheet of (2). In the trained net please eliminate the upper hidden neuron. Tick the classifications for W and A stimuli in the work sheet of (2) and check the training curve of the lesioned net. In another trained net eliminate the middle hidden neuron and proceed as above. In another trained net eliminate the lower hidden neuron and proceed appropriately.
(6) Finished experiment for IM=10x10; HL=5. In the diagrams — shown in the figure below — the corresponding eW ,eAvalues for W and A stimuli of different length (obtained with the manual test method) are calculated and plotted already: for the intact net and for four trained nets after elimination of one of the 5 neurons of the hidden layer. Discuss the results:
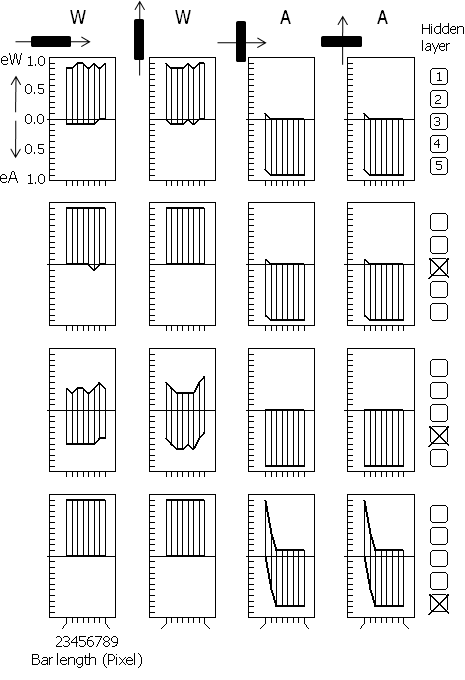
(7) Compare the learning curves for IM=10x10; HL=1, 2, 5, 8, or 10.
(8) Repeat experiment (1). After training, please check the net’s detection in response to a stimulus the net was not trained for: a W stimulus in terms of a bar of an edge length of 5 pixels; over the right or left edge of the bar add a spot of 1 x 1 pixel. (The toad’s behavior in response to this stimulus configuration is shown in the Video-Preview /Vorschau). The difference picture (produced manually) looks like:

Questions:
a) Is one neuron in the hidden layer sufficient for W vs. A detection?
b) Discuss the advantages of several neurons in the hidden layer? Reconsider this aspect in the sense of “division of work”.
c) Is there an optimal number of HL neurons?
d) Does the W vs. A detection acuity depend on the length of W and A stimuli, respectively?
e) Is the detection acuity for W stimuli different from the one for A stimuli, and if so, why?
f) Do neurons of the hidden layer — after training — hold specific functions for feature detection? If certain hidden layer neurons do not seem to influence the net’s detection ability after training, are those neurons just redundant, i.e. needless for the net during training?
g) Why is the course of a training curve of a net with one neuron in the hidden layer different from the training curve of a lesioned net in which one of two HL neurons was eliminated?
h) How can the results of experiment (7) be explained?
i) May a trained net develop unexpected properties?
Project B: Detection of the length of worms and anti-worms — investigating the course of learning curves and the acuity of bar length detection
Do not use matrices greater than 7 x 7 pixels in Project B. In the settings of the net options-2, leave all settings except “Extras”: since the net should evaluate the length of wormlike and anti-wormlike bars, please let “Nur Wurn/Antiwurm” blank (i.e., no X):
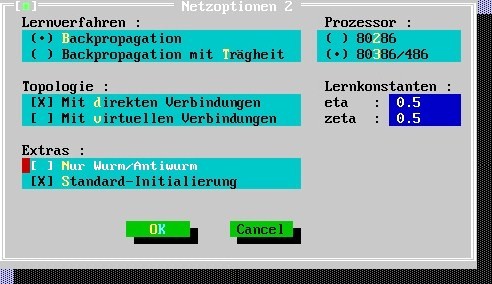
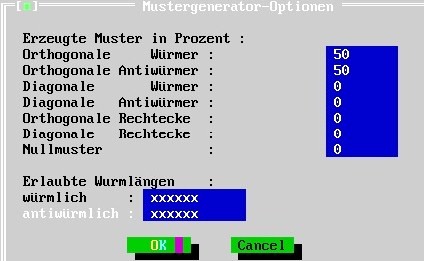
Leave all settings in this window except one: under “erlaubte Wurm/Antiwurm-Längen”, the size of the IM should fit the bar length of the W and A stimuli, i.e. in the present case: 6 pixels; please use the Del-shift button in order to cut pixels accordingly [use the x button in order to extend, if necessary]:
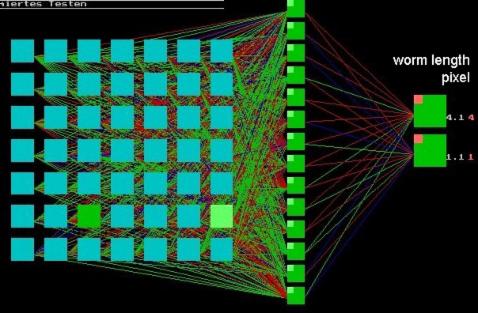
The Figure shows a trained net consisting of IM=;7 and HL=14 in response to a wormlike moving bar of 4 pixel lengths; the net’s calculation: 4.1 (see upper output neuron):
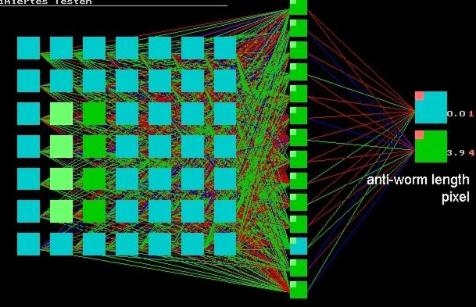
The Figure shows the same net in response to an anti-wormlike moving bar of 4 pixel lengths; the net’s calculation: 3.9 (see lower output neuron):
Learning curve: The net is trained after 195,000 training steps at an error of 4.20%:
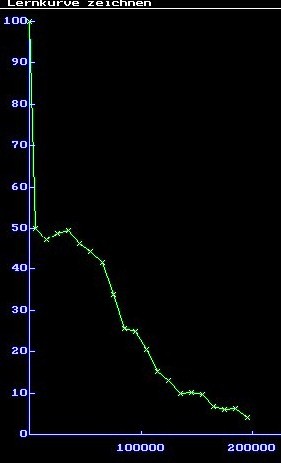
Prior to training you might eliminate certain pixel(s) from the end of a bar (using the Del button) under “erlaubte Wurm/Antiwurm-Längen”; after training you will check the acuity of the net in scaling such bar. For example, change settings: 3 pixels for anti-worm; 6 pixels for worm:
Various questions should be addressed to the appropriate experiments
Experiments:
(1) Please train nets with the following topologies: IM=5x5; in different nets vary HL= 1, 2, 5, and 10, respectively. Discuss the learning curves of the four nets.
(2) Vary the relationship IM : HL in different nets, e.g.: {IM= 7x7; HL=14}; {IM=7x7; HL=7}; {IM=7x7;HL=4}. Compare the learning curves.
(3) Train a net with the topology IM=7x7; HL=14 and check the length detection acuity for W and A stimuli.
Questions:a) Compare the learning curves of Project A (W-bar vs. A-bar detection) and Project B (bar length detection) for different sizes of the HL and different relationships IM : HL.
b) Discuss the differences with respect to optimization: necessity, sufficiency, and redundancy. Compare — in concert with the data obtained from Project A — the ontogenetic development of our brain. Consider advantages and disadvantages of neuronal death.
_____________________________________________________________________
Appendix
AND condition
In the following it will be shown that one artificial neuron (so-to-speak: an artificial neuronal net consisting of one layer with just one neuron) can make a decision in a manner of an AND gate or an OR gate. To introduce the problem, consider the following electrical circuit including a power source, a light bulb, and two switches S1 and S2 arranged in serial order. Only if both switches S1 AND S2 are pressed, the light is turned on.
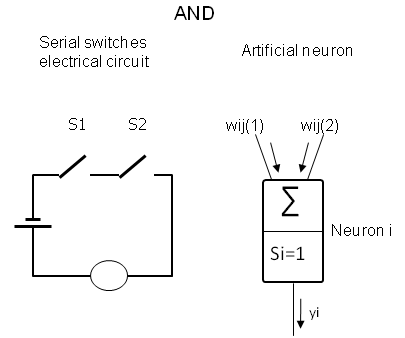
Such an AND condition can be simulated by means of an artificial neuron i which receives two inputs (equivalent to S1 and S2), namely xj(1) and xj(2) . Each input is multiplied with a synaptic weight wij(1) and wij(2). Set for xj(1) = xj(2) = wij(1) = wij(2) =1. Hence each weighted input =1. According to the equation
yi = fi ∑(xj * wij – si)
a threshold si will be subtracted from the
summated weighted inputs.
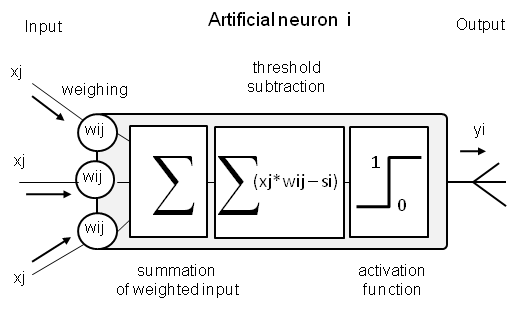
Furthermore, an activation function fi(x) allows the output to reach yi=1 for x≥1 and yi=0 for x≤1. The equation describes the AND condition for si=1:
Inputs Output
_________________________
xj(1) xj(2) yi
_________________________
0 0 0
1 1 1
0 1 0
1 0 0
_________________________
Unlike the electrical circuit, the artificial neuron
will only provide an output if both inputs are present simultaneously. It thus
behaves like a coincidence detector.
In neurobiology, coincidence detection is a mechanism to encode neural information based on two separate inputs converging on a common target neuron. The coincident timing of these inputs allows to push the membrane potential of the target neuron over the threshold (si) required to create an output. If the two inputs occur at different times, the effect of the first input has time to drop significantly, so that the effect of the second input will not be sufficient to create an output of the target neuron.
OR condition
Different from the electrical circuit described above,
here the two switches S1, S2 are arranged in a parallel fashion.
In this case, the light is turned on if S1
OR S2 is pressed.
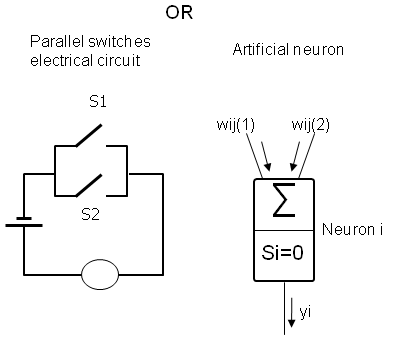
This OR condition can be simulated by means of the same artificial neuron provided si=0:
Inputs Output
_________________________
xj(1) xj(2) yi
_________________________
0 0 0
1 0 1
0 1 1
However:
1 1 1
_________________________
XOR condition
However, there is a problem with the OR condition
described above: if both inputs arrive simultaneously, the neuron, too,
provides an output. The output is not exclusive either to the one input or to the
other input. This is called the “XOR problem”. The problem can be solved only by
introducing another layer of artificial neurons involving mutual inhibition of
the two inputs: if one input is active, the other one will be cancelled and vice versa. If both inputs are active simultaneously,
they will cancel each other.
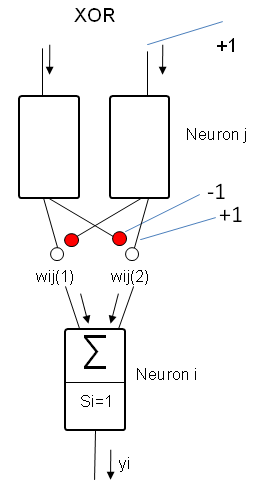
This shows that the complexity factor of problems to some extent determines the number of layers of neurons in a neuronal network.